The Euler project is a website that contains problems that are intended to be solved by computer programs. In this post I’ll be examining a few problems I found interesting and detail my solutions.
Fibonacci Sequence
The Fibonacci sequence is a sequence of numbers where each number is defined as being the sum of the previous two numbers, starting from 0 and 1. The sequence begins: 0, 1, 1, 2, 3, 5….. and continues infinitely. This sequence is often found in both nature and mathematics, so much research has been done on its properties and potential scientific applications.

The problem I am personally going to examine is the following; how far in the Fibonacci sequence do you need to go before finding a number that exceeds 1000 digits?
I began by creating a Python generator that produces the values of the Fibonacci sequence. This allows me to iterate over the generator and continually produce consecutive values.
def fibonacci():
"""
Create a python generator to yield the values of the Fibonacci sequence.
Returns:
(int): A given integer value of the Fibonacci sequence.
"""
n_1, n_2 = 0,1
while True:
yield (n_1 + n_2)
n_1, n_2 = n_2, n_1 + n_2 #Update values of n-1 and n-2.
Since I now had a way to create the values in the sequence, all I needed to do was calculate the values and check how many digits each value had. Once the program finds a number with 1000 digits it stops and displays the answer. It ultimately takes 4782 iterations of the Fibonacci sequence to produce a number with at least 1000 digits.
# Create fibonacci generator and start counting the indices.
f = fibonacci()
index = 1
# Iterate over the generator to produce values until you get to a value with a length of 1000.
for x in f:
index += 1
length = (int(math.log10(x))+1) #Check the length of the number.
if (length == 1000):
print ('The first index of the Fibonacci sequence to break 1000 digits is {}. It has a length of {} digits.'.format(index, length))
break
Lychrel Numbers
If we take 47, reverse and add, 47 + 74 = 121, which is palindromic.
Not all numbers produce palindromes so quickly. For example,
349 + 943 = 1292
1292 + 2921 = 4213
4213 + 3124 = 7337
That is, 349 took three iterations to arrive at a palindrome.
Mathematicians theorize that some numbers never produce a palindrome through this repetition of reversal and addition. Numbers with this property are called Lychrel numbers. The vast majority of numbers that eventually become a palindrome take less than 50 iterations of reversal and addition to do so. For this problem, I determined how many numbers under 10000 are Lychrel numbers. This calculation assumed that a number is a Lychrel number if it doesn’t become a palindrome within 50 iterations.
I began by creating functions to sum a number and its reverse.
def reverse(number):
"""
Takes a number, converts it to a string and reverses it, then converts it back an int.
Parameters:
number (int): An integer.
Returns:
(int): Integer of the reverse of number.
"""
reversed = int(str(number)[::-1])
return(reversed)
def sum_reverse(number):
"""
Sums an integer and its reverse.
Parameters:
number (int): An integer.
Returns:
(int): Integer containing the sum of a number and its reverse.
"""
return(number + reverse(number))
Next, I had to create a function to check if a given number is a palindrome. This works by reversing the number and checking for equality.
def is_palindrome(number):
"""
Checks if a number is a palindrome and returns a boolean based on the result.
Parameters:
number (int): An integer.
Returns:
(boolean): Boolean indicating if the number is a palindrome.
"""
if (reverse(number) == number):
return True
else:
return False
The last function repeats the reversal and summation process 50 times and checks if the output of each iteration is a palindrome.
def is_lychrel(number):
"""
Determines if a given number input is a Lychrel number within 50 iterations.
Returns a boolean value corresponding to Lychrel status.
Parameters:
number (int): An integer.
Returns:
bool_lychrel (boolean): Boolean indicated if the number is a Lychrel number.
"""
new_num = number
bool_lychrel = True
for i in range (50):
new_num = sum_reverse(new_num)
if is_palindrome(new_num): #Change flag to false if any numbers produced are palindromes.
bool_lychrel = False
return(bool_lychrel)
Finally, I loop over the numbers from 1-10000 and append their Lychrel status to a list. I can then sum the list to determine how many numbers are Lychrel- this produces a final answer of 249.
#Iterate over the first 10000 numbers to see how many lychrel numbers there are.
lychrel_list = []
for i in range(0,10000):
lychrel_list.append(is_lychrel(i))
print("The number of Lychrel numbers from 1 to 10000 is {}.".format(sum(lychrel_list)))
Dice Game
The last problem I chose to solve was a bit trickier than the previous ones. The problem is as follows:
Peter has nine four-sided dice, each with faces numbered 1, 2, 3, 4. Colin has six six-sided dice, each with faces numbered 1, 2, 3, 4, 5, 6.
Peter and Colin roll their dice and compare sums: the highest sum wins. The result is a draw if the sums are equal. What is the probability that Peter beats Colin? Give your answer accurate to 7 decimal places.

My initial approach to solve this problem was a Monte Carlo simulation, that is, I would simulate the game being played over and over again and estimate Peter’s win rate. The more simulations I ran the more accurate (in theory) the estimate would be. I began this approach by creating a function that simulates each player’s throws; the function “rolls the dice” for each player and compares the sum of the dice to produce the winner.
def play_game():
"""
Simulates two players throwing dice. One player has 9 dice with sides 1-4 and another has 6 dice with sides 1-6.
A value is returned that says if the player with 9 dice (pete/peter) wins.
Returns:
winner (int): An integer 1 or 0 indicating whether or not the first player has won. 1 indicates victory.
"""
#Calculate the scores for each player
pete_score = np.sum(np.random.randint(low = 1, high = 5, size = 9))
colin_score = np.sum(np.random.randint(low = 1, high = 7, size = 6))
#Compare scores to see who wins
if pete_score > colin_score:
winner = 1.0
else:
winner = 0.0
return(winner)
Now that I could model one throw I could throw the dice many times to try to estimate Peter’s true win percentage. I decided to run 1000000 simulations of the game.
#Run 1000000 simulations of the game.
winners = []
for i in range(1000000):
winner = play_game()
winners.append(winner)
#Print the result. It's accurate to the first ~3 decimal places.
print("Pete's win probability is about {}.".format(np.mean(winners)))
As you can see below, the model converged rather quickly. These simulations gave an estimate of Peter’s win rate being 0.5739220.
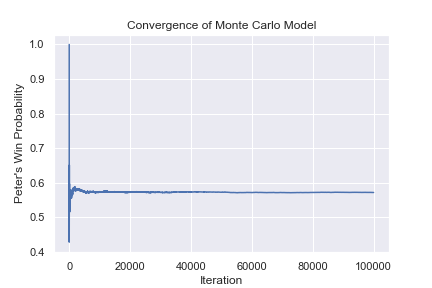
Unfortunately, however, the answer I produced was only accurate to the first 3 decimal places. I needed to find a more exact way to estimate the win rate.
One way to determine the win rate is to explicitly calculate the probability of each sum appearing with a given dice combination. Luckily, I was able to find this formula that can be used to compute the probability of getting a sum of k from rolling n dice with s sides.

I implemented this formula in the following function.
def prob_outcome(k, s, n):
"""
Calculate the probability of a sum k occurring given n dice with s sides.
Returns a float value ranging from 0-1.
Parameters:
k (int): The integer sum you want to find the probability of.
s (int): An integer corresponding to the number of sides on each die.
n (int): The integer number of total dice.
Returns:
(float) : The probability of the sum k occuring given n dice with s sides.
"""
prob = 0
possible_vals = math.pow(s,n)
top_val = math.floor((k - n)/s)
for i in range(0, top_val +1):
prob += math.pow(-1, i) * special.comb(n,i) * special.comb(k-s*i-1,n-1)
return prob/possible_vals
This second function uses the previous one to generate pairs of sums and their associated probabilities.
def find_probs(s, n):
"""
Create a dictionary of sums k with their associated probabilities for n dice with s sides.
Parameters:
s (int): The number of sides on each die.
n (int): The number of dice.
Returns:
prob_dict (dict): A dictionary containing pairs of sums (k) and their associated probabilites of occurrence.
"""
prob_dict = {}
for i in range(n, s * n + 1):
prob_dict[i] = prob_outcome(i, s, n)
return(prob_dict)
If we assume each player’s dice rolls are independent, the chance of that combination of rolls occurring is just the two probabilties multiplied together. The next two functions work together to produce a matrix of the joint probabilities of rolling various sums. The first portion creates two arrays containing the probability of each outcome for both players. The second takes those two arrays and uses them to produce a matrix of joint probabilities.
def label_creation(prob_dict):
"""
Create an array of outcomes and a list of their associated probabilities of occurrence.
Parameters:
prob_dict (dict): An dictionary with key value pairs of sums and their probabilities of occurrence.
Returns:
(array): An array containing probabilities.
(array): An array containing sums.
"""
return np.array(list(prob_dict.keys())), np.array(list(prob_dict.values()))
def create_matrix(prob1, prob2):
"""
Create a matrix of the product of the probabilities of seperate dice rolls.
This will compute the probability of all combinations of their sums.
Parameters:
prob1 (array): A numpy array containing the probability of each roll for player 1.
prob2 (array): A numpy array containing the probability of each roll for player 2.
Returns:
prob_matrix (array): A matrix containing the joint probabilities of each roll combination.
"""
prob_matrix = np.outer(prob1, prob2)
return(prob_matrix)
Here is a heatmap of the probability of each combination of dice rolls. It looks like Peter may win slightly more often than Colin.
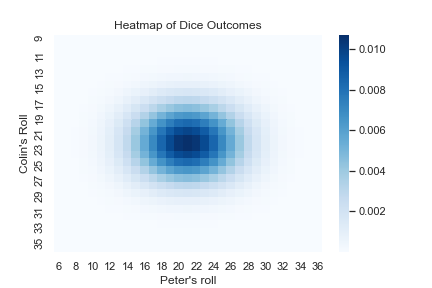
Now that I had the probabilities of all possible outcomes, all that was remained was to add up the probabilities associated with Peter winning.I started by writing a function to iterate over the matrix of outcomes and put a value of True wherever Peter won. By multipling these boolean values with the probabilities I was able to produce a matrix that contained only the probabilities that corresponded to Peter’s victory. Adding these numbers up produced the final answer: 0.5731440767829801.
def win_matrix(outcomes1, outcomes2):
"""
Compare the possible outcomes in each row and column to produce a matrix that shows who wins.
Parameters:
outcomes1 (array): An array containing the possible sums for the first player.
outcomes2 (array): An array containing the possible sums for the second player.
Returns:
win_matrix (arary): An array filled with boolean values indicating if a given roll combination is a win for player 1.
"""
d1 = outcomes1.shape[0]
d2 = outcomes2.shape[0]
win_matrix = np.zeros((d1,d2))
for i in range(d1): #Rows
for j in range(d2): #Columns
if outcomes1[i] > outcomes2[j]: #Compare values
win_matrix[i,j] = True
else:
win_matrix[i,j] = False
return(win_matrix)
def win_prob(win_matrix, prob_matrix):
"""
Multiply the wins with the probability of the win occurring and sum them.
This produces the overall win rate.
Parameters:
win_matrix (array): A boolean array showing if each roll is a win for player 1.
prob_matrix (array): An array containing the joint probabilities of each pair of rolls.
Returns:
(float): The proportion of the time that player one wins.
"""
return (np.sum(win_matrix * prob_matrix))
Sources
Project Euler: https://projecteuler.net/
Dice Formulas: https://mathworld.wolfram.com/Dice.html